時系列データにおいてXの効果をどのように捉えるか
時系列データやパネルデータを分析するときの主要な関心の1つは、変化する独立変数が従属変数に対していかなる効果を与えるのかを明らかにすることにあります。たとえば社会学だと、「結婚することによって幸福度がどのように変化するか」であるとか、「転職することによって賃金は上がるのか」といった問いが例として挙げられます。
ある個体(id)について、複数時点のデータを収集した結果、この個体は、時点4において状態Xの変化を経験したとします。このときのデータは以下のように表すことができます。
── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr 1.1.4 ✔ readr 2.1.5
✔ forcats 1.0.0 ✔ stringr 1.5.1
✔ ggplot2 4.0.1 ✔ tibble 3.2.1
✔ lubridate 1.9.4 ✔ tidyr 1.3.1
✔ purrr 1.0.4
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
id <- c(1, 1, 1, 1, 1, 1, 1)
time <- c(1, 2, 3, 4, 5, 6, 7)
x <- c(0, 0, 0, 1, 1, 1, 1)
df <- tibble(id, time, x)
df
# A tibble: 7 × 3
id time x
<dbl> <dbl> <dbl>
1 1 1 0
2 1 2 0
3 1 3 0
4 1 4 1
5 1 5 1
6 1 6 1
7 1 7 1
なお今回は簡単のため、Xは基本的に0から1にしか変化しない(不可逆的な変化をする)離散的な変数とします。たとえば、未婚→既婚(既婚から未婚にはなれない)、転職経験なし→転職経験あり(経験ありからなしにはなれない)、30歳未満→30歳以上(年齢は常に上がるので)、などといった状態の変化を考えると良いと思います。
今回は、Xが従属変数Yに対して与える効果をより柔軟に考えるための例を、いくつか考えてみます。これ以降の説明のために、上記のデータから以下のようなデータを作ります。
df <- df %>%
group_by(id) %>% # idごとにコードを実行するためにgroup_by()
mutate(change = if_else(x == 1 & lag(x, n = 1) == 0, time, 0)) %>%
mutate(change = max(change)) %>%
mutate(tchange = time - change) %>%
mutate(a = if_else(tchange < 0, 0, tchange)) %>%
mutate(a_sq = a^2) %>%
mutate(b = log(a+1)) %>%
mutate(c = if_else(tchange > 0, 0, tchange))
df
# A tibble: 7 × 9
# Groups: id [1]
id time x change tchange a a_sq b c
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 1 0 4 -3 0 0 0 -3
2 1 2 0 4 -2 0 0 0 -2
3 1 3 0 4 -1 0 0 0 -1
4 1 4 1 4 0 0 0 0 0
5 1 5 1 4 1 1 1 0.693 0
6 1 6 1 4 2 2 4 1.10 0
7 1 7 1 4 3 3 9 1.39 0
例1 Xの効果はすぐに現れ、かつ持続する
もっとも基本的なのは、Xをそのまま独立変数として投入することです。式で表すと以下のようになります。
\[
Y = \beta_0 + \beta_1X
\]
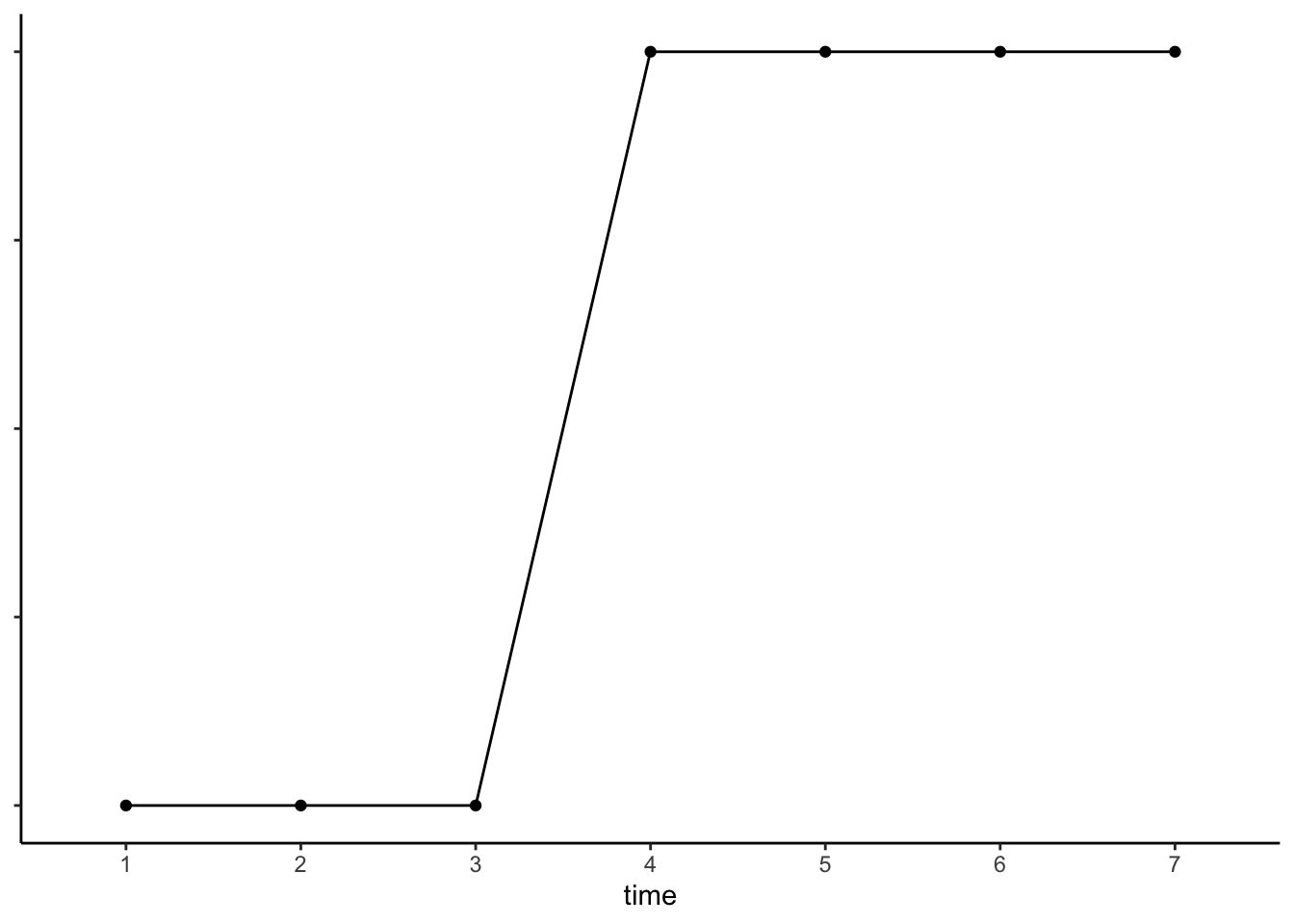
この場合、X = 0からX = 1へと変化したとき、Yの変化もそれに対応して即座に現れ、かつそれが持続するということを想定しています。図で表すと以下の実線や点線のようになります。
value <- c(1,1,1,2,2,2,2)
ydf <- tibble(value)
df %>%
bind_cols(ydf) %>%
ggplot(aes(x = factor(time), y = value, group = "time")) +
geom_line() +
geom_point() +
theme_classic() +
theme(axis.title.y = element_blank(),
axis.text.y = element_blank()) +
labs(x = "time")
もしXの効果が時間の経過にともなって変化していた場合、Xの効果は、X = 0のときのYの平均値と、x = 1のときのYの平均値の差として表されることになります。このモデルは、Xの効果を表すにあたり、もっとも単純なものといえます。
例2 Xの効果は徐々に現れる
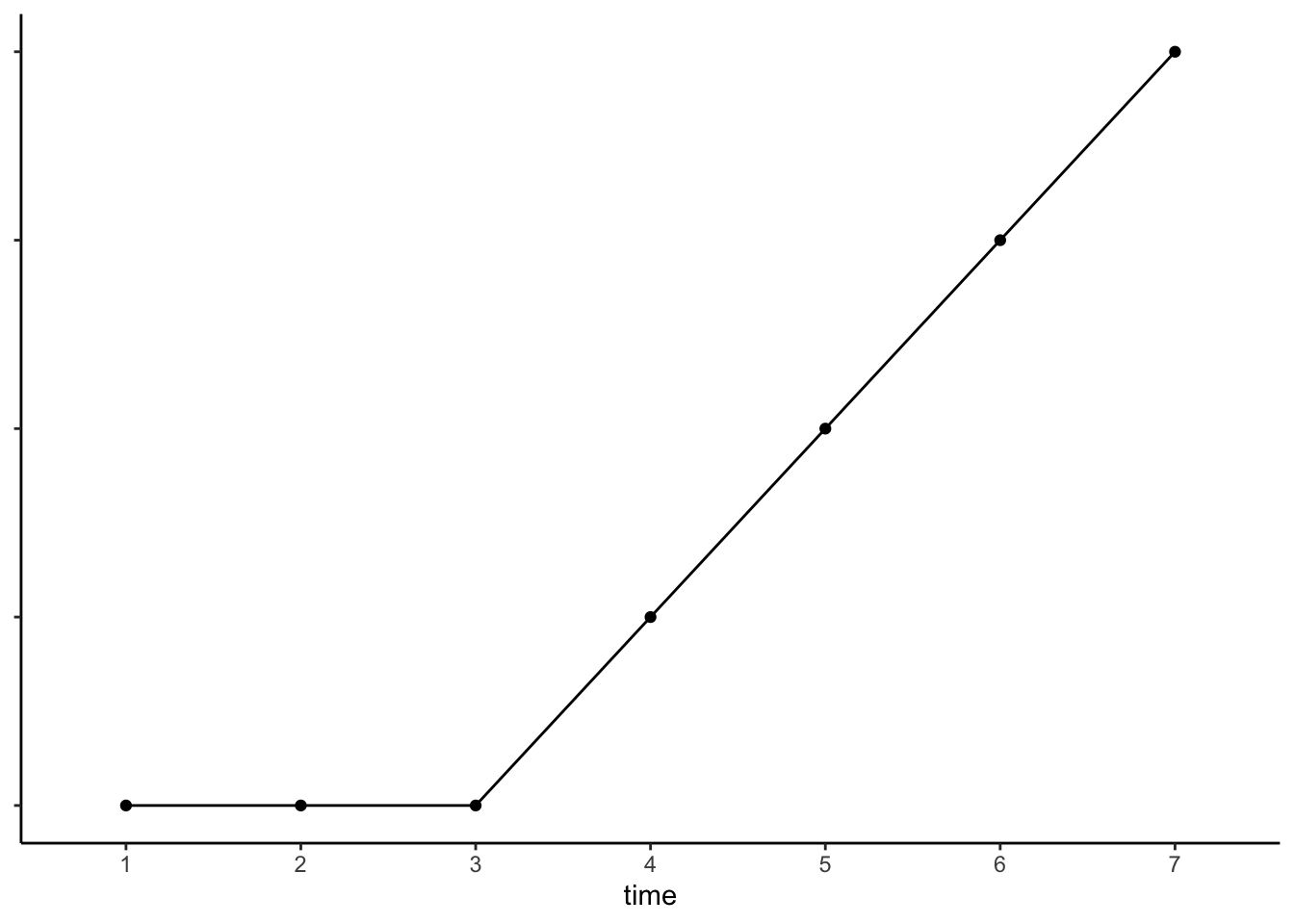
一方で、Xの効果はX = 0からX = 1となった直後から現れるのではなく、時間の経過とともに徐々に現れるということも考えられます。これは、変数Aおよび図を用いて、以下のように表されます。
\[
Y = \beta_0 + \beta_1A
\]
value <- c(1,1,1,2,3,4,5)
ydf <- tibble(value)
df %>%
bind_cols(ydf) %>%
ggplot(aes(x = factor(time), y = value, group = "time")) +
geom_line() +
geom_point() +
theme_classic() +
theme(axis.title.y = element_blank(),
axis.text.y = element_blank()) +
labs(x = "time")
このモデリングは、Xへの暴露(Exposure, duration)期間がYへの効果をもたらす主要な要因となっている、という想定を置いています。たとえば、「失業がメンタルヘルスに負の影響を与える」という因果関係について考えます。このとき、有業から失業状態に変化した直後はメンタルヘルスに影響はないものの、失業期間が長期化するほどメンタルヘルスは悪化していく、という可能性があります。もし失業がメンタルヘルスに与える影響がこのようなものであるとしたら、例1のように有業(X = 0)と失業(X = 1)とを単純に比較することは、失業の負の効果は捉えられるものの、メンタルヘルスを悪化させるメカニズムを的確に表すことにならないといえます。
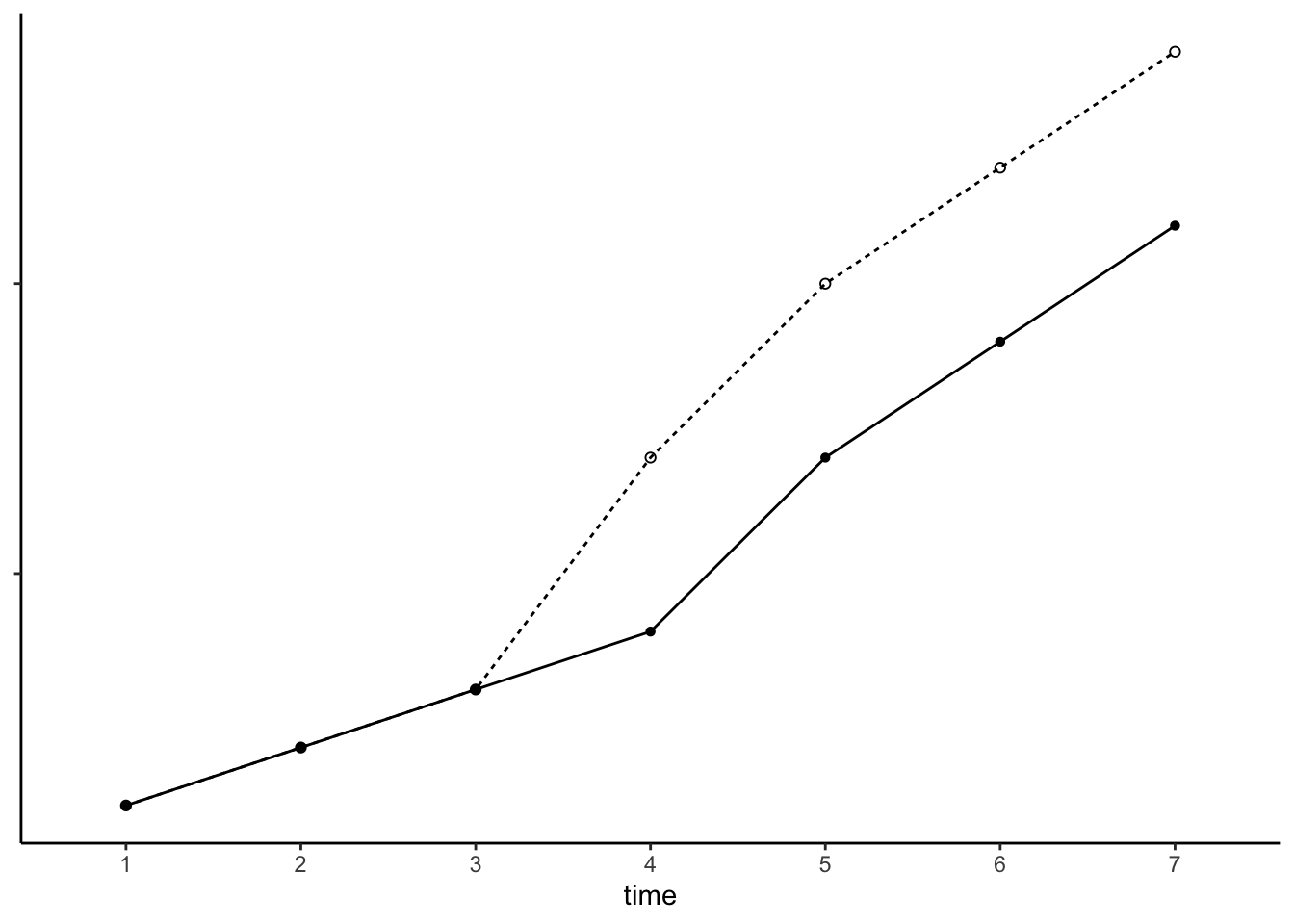
例3 Xの効果はすぐに現れ、かつ徐々に変化する
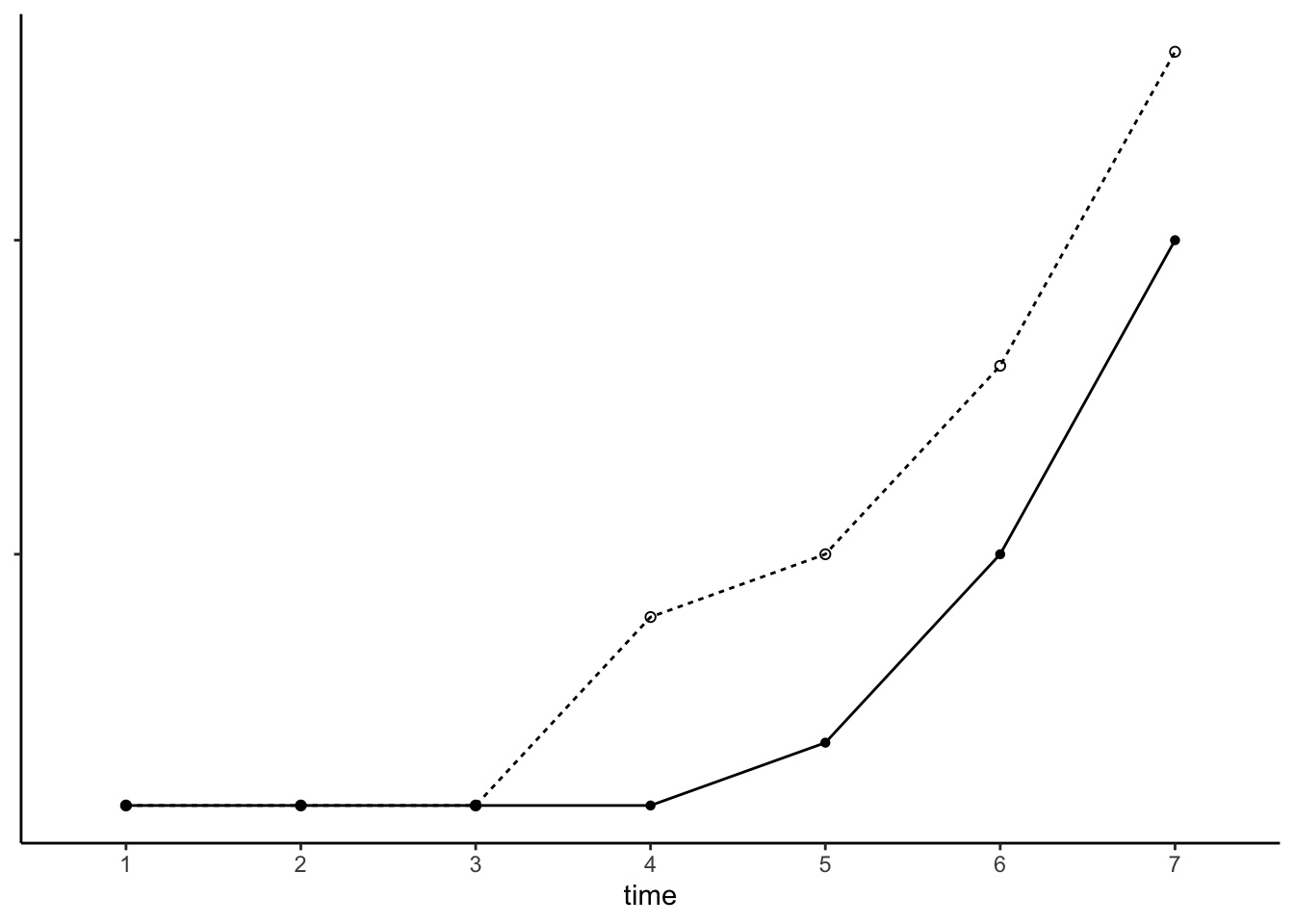
以上紹介した例1と例2のような効果が共存するという場合も考えられます。つまり、X = 0からX = 1に変化した直後に大きな変化があり、かつその後、時間の経過に伴ってさらにその効果が変化していくというものです。こうした関係は、以下のような式と図で表すことができます。
\[
Y = \beta_0 + \beta_1X + \beta_2A
\]
value <- c(1,1,1,5,4,3,2)
ydf <- tibble(value)
df %>%
bind_cols(ydf) %>%
ggplot(aes(x = factor(time), y = value, group = "time")) +
geom_line() +
geom_point() +
theme_classic() +
theme(axis.title.y = element_blank(),
axis.text.y = element_blank()) +
labs(x = "time")
\(\beta_1\)はx = 0からX = 1となるタイミングでのYの変化(インパクト)を、\(\beta_2\)はX = 1となってから、時間が経過するにともなって変化する傾向をそれぞれ捉えています。\(\beta_1\)が0に近づくほど例2に近い関連があり、\(\beta_2\)が0に近づくほど例1に近い関連があるといえます。
実線のような例は、先ほどの失業とメンタルヘルスの関連が考えられます。有業(X = 0)から失業(X = 1)となるタイミングで大きくメンタルヘルスが悪化し、それが失業期間の長期化にともなってさらに悪化していく、という関連が考えられる場合は、このモデルがより適切といえます。
点線のような例として、結婚と幸福度の関係が考えられます。未婚(X = 0)から既婚(X = 1)となるタイミングでは幸福度が大きく高まるものの、時間の経過にしたがって幸福度は徐々に低下していく(Honeymoon effect)といった場合がこれに当てはまります。
例4 Xの効果は非線形に変化する(2乗)
Xの効果が時間の経過にともなって変化していくとして、その変化のパターンは線形である必要はなく、さまざまな関数型を想定することができます。例2のような関連を非線形(2次曲線)に拡張した場合は、以下のようなモデルになります。
\[
Y = \beta_0 + \beta_1A + \beta_2A^2
\]
同様に、例3のような関連を非線形に拡張した場合は以下のようなモデルになります。
\[
Y = \beta_0 + \beta_1X + \beta_2A + \beta_3A^2
\]
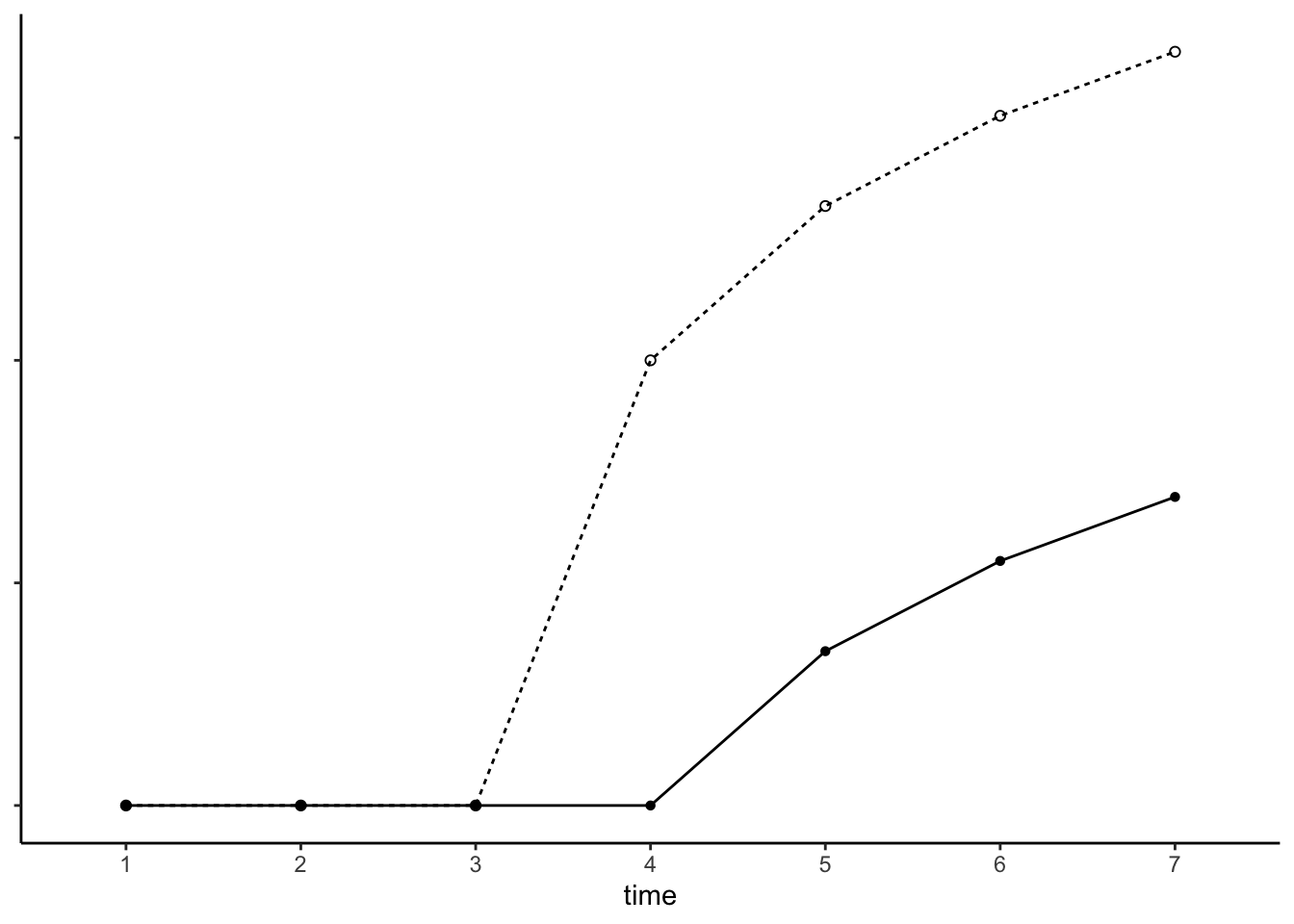
たとえば前者は実線のように、後者は点線のように図示できます。
value <- c(1,1,1,1,2,5,10)
ydf <- tibble(value)
df1 <- df %>% bind_cols(ydf) %>% mutate(sample = "Sample 1")
value <- c(1,1,1,4,5,8,13)
ydf <- tibble(value)
df2 <- df %>% bind_cols(ydf) %>% mutate(sample = "Sample 2")
df1 %>%
bind_rows(df2) %>%
ggplot(aes(x = factor(time), y = value, group = sample, linetype = sample, shape = sample)) +
geom_line() +
geom_point() +
scale_shape_manual(values = c(16, 1)) +
theme_classic() +
theme(axis.title.y = element_blank(),
axis.text.y = element_blank(),
legend.position = "none") +
labs(x = "time")
2次曲線を用いているので、Xの変化のあとしばらくはYが上昇傾向を示したのち、しばらくするとYは減少傾向に転じるといった関係をとることもあり得ます。
例5 Xの効果は非線形に変化する(log)
もちろん、2次曲線以外の非線形な変化も想定することができます。他の例として、経過時間の自然対数を取った以下のモデルを考えることができます。
\[
Y = \beta_0 + \beta_1B
\]
\[
Y = \beta_0 + \beta_1X + \beta_2B
\]
value <- c(1,1,1,1 + log(1),1 + log(2),1 + log(3),1 + log(4))
ydf <- tibble(value)
df1 <- df %>% bind_cols(ydf) %>% mutate(sample = "Sample 1")
value <- c(1,1,1,3 + log(1),3 + log(2),3 + log(3),3 + log(4))
ydf <- tibble(value)
df2 <- df %>% bind_cols(ydf) %>% mutate(sample = "Sample 2")
df1 %>%
bind_rows(df2) %>%
ggplot(aes(x = factor(time), y = value, group = sample, linetype = sample, shape = sample)) +
geom_line() +
geom_point() +
scale_shape_manual(values = c(16, 1)) +
theme_classic() +
theme(axis.title.y = element_blank(),
axis.text.y = element_blank(),
legend.position = "none") +
labs(x = "time")
対数変換することで、最初の方は大きく変化するが、時間の経過にともなって変化が徐々に緩やかになる(ただし2次曲線のときと違って正負が反転することはない)、といった関連を捉えることができます。
例6 Xの前後で時間の効果が変化する(spline)
ここまでは、Xの効果は常にX = 1となってから現れ始めることが想定されていました。しかし、Xの効果はX = 0のときからすでに現れており、X = 1となってからその効果のパターンが変化するという場合も考えられます。
value <- c(1,2,3,4,7,9,11)
ydf <- tibble(value)
df1 <- df %>% bind_cols(ydf) %>% mutate(sample = "Sample 1")
value <- c(1,2,3,7,10,12,14)
ydf <- tibble(value)
df2 <- df %>% bind_cols(ydf) %>% mutate(sample = "Sample 2")
df1 %>%
bind_rows(df2) %>%
ggplot(aes(x = factor(time), y = value, group = sample, linetype = sample, shape = sample)) +
geom_line() +
geom_point() +
scale_shape_manual(values = c(16, 1)) +
theme_classic() +
theme(axis.title.y = element_blank(),
axis.text.y = element_blank(),
legend.position = "none") +
labs(x = "time")
図の実線のような場合がこれに当たります。Xが変化する以前と以後では、時間の経過に伴うYの値の変化が異なっていることがわかります。
\[
Y = \beta_0 + \beta_1Time + \beta_2Time \times X
\]
Xが変化した時点でYが一定程度変化するものと想定する場合、すなわち図の点線のような場合には、以下のようなモデルになります。
\[
Y = \beta_0 +\beta_1Time + \beta_2X + \beta_3Time \times X
\]
このモデリングの場合、係数\(\beta_3\)は、「傾き\(\beta_1\)と比較してどの程度異なっているのか」を表すことになり、交互作用効果のように解釈することになります。ですから、実質的な傾きが統計的に有意に0と異なるかどうかを直接検定することはできません。
もう一つ、以下のようなモデリングを考えることができます。
\[
Y = \beta_0 + \beta_1C + \beta_2A
\]
CはXの変化以前の、AはXの変化からの経過年数を表す以下のような変数でした。
df %>%
select(id, time, x, c, a)
# A tibble: 7 × 5
# Groups: id [1]
id time x c a
<dbl> <dbl> <dbl> <dbl> <dbl>
1 1 1 0 -3 0
2 1 2 0 -2 0
3 1 3 0 -1 0
4 1 4 1 0 0
5 1 5 1 0 1
6 1 6 1 0 2
7 1 7 1 0 3
こちらもやはり、Xが変化した時点でYが一定程度変化すると考えると、以下のようなモデルとなります。
\[
Y = \beta_0 + \beta_1X + \beta_2C + \beta_3A
\]
こちらのモデリングの場合、係数\(\beta_2\)および\(\beta_3\)は、「傾き0と比較してどの程度異なっているのか」を表すことになります。こちらは、x=0のときとX=1のときの実質的な傾きが統計的に有意に0と異なることを検定できますが、\(\beta_2 \neq \beta_3\)の検定はできません。
例7 Xからの経過時間ごとにダミー変数を作る
さて、以上のような関連があることを見破るためには、ダミー変数を使った探索的な分析が有効です。例えば以下のように、Xの変化からの経過時間ごとに変数を作成することが考えられます。
\[
Y = \beta_0 + \beta_1D_{X=-3} + \beta_2D_{X=-2} + \beta_3D_{X=-1} + \beta_4D_{X=0} + \beta_5D_{X=1} + \beta_6D_{X=2} + \beta_7D_{X=3}
\]
ダミー変数を使ったモデリングは時間を連続変数としてモデリングするよりもさらに柔軟にパラメータを推定できる点で優れているといえます。適当な関数形がないなど、連続変数を使うよりもダミー変数のほうがより望ましい場合も多いです。
ただし、カテゴリを細かくすればするほど推定が不安定になるという点には注意が必要です。とくにYが離散変数で、ロジットモデルやプロビットモデルを使って分析している場合には、ダミー変数の各カテゴリにY=0とY=1のケースがいずれも含まれていないといけないので(いわゆるゼロセルの問題)、ある程度粗いカテゴリを設定しつつ分析する必要があります。
Xの変化以前を考慮するときの問題
以上、時間による効果の変化を考えるための方法について考えてきました。ここではとくにXの変化以前を考慮に入れる場合の問題について扱います。
一般に、Xが時変の変数である場合には、X = 1が観察できない(センサリング)という問題があります。このことは、とくにXの変化以前を考える際に、何と何を比較していることになるのかが分かりにくくなる、という問題を生じさせます。たとえば、Xの変化を経験したサンプルと経験していないサンプルがいずれも含まれている以下のようなデータセットを考えます。
id <- c(2,2,2)
time <- c(1,2,3)
x <- c(0,0,0)
tchange <- c(NA_real_, NA_real_, NA_real_)
id2df <- tibble(time, x, tchange)
df %>%
bind_rows(id2df) %>%
mutate(before_event1 = if_else(time - tchange == 1, 1, 0)) %>%
replace_na(list(before_event1 = 0)) %>%
mutate(before_event2 = if_else(time - tchange == 1, 1, 0)) %>%
mutate(before_event3 = if_else(lead(x, n = 1) - x == 1, 1, 0)) %>%
mutate(before_event3 = if_else(x == 1, 0, before_event3)) %>%
select(id, time, x, tchange, before_event1, before_event2, before_event3)
# A tibble: 10 × 7
# Groups: id [2]
id time x tchange before_event1 before_event2 before_event3
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 1 0 -3 0 0 0
2 1 2 0 -2 0 0 0
3 1 3 0 -1 0 0 1
4 1 4 1 0 0 0 0
5 1 5 1 1 0 0 0
6 1 6 1 2 0 0 0
7 1 7 1 3 0 0 0
8 NA 1 0 NA 0 NA 0
9 NA 2 0 NA 0 NA 0
10 NA 3 0 NA 0 NA NA
いま、Xの変化の1時点前を示すダミー変数を作成したいとします。id2の個人については、Xの変化が観察できていません。そうすると、Xの変化からの経過時間もわからないので、1時点ダミーもid1と同じようには定義することができません。この場合、以下の3つの方法があります。
1時点前(1):Xの変化を観察できていない場合については0を代入する。
この場合、1時点前ダミーの効果は、1行目、2行目、8行目、9行目、10行目を参照カテゴリとした場合の効果を意味する。
利点:サンプルサイズを多く確保できる。
欠点:比較の対象が異質な集団で構成される(X = 1となった個人における1時点以上前の行 + まだX = 1となっていない個人の行すべて)ため、解釈がより難しくなる。id2の個人はtime = 4のときにX = 1となるかもしれず、その場合、time = 3はX=1となる1時点前であるにもかかわらず、誤って1時点前でない、と判断してしまうことになる。
1時点前(2):Xの変化を観察できていない場合はすべて欠損とする。
この場合、1時点前ダミーの効果は、1行目、2行目を参照カテゴリとした場合の効果を意味する。
利点:誤って1時点前でない、と判断することを防いでいる。またX = 0 と X = 1の両方を経験した個人のみを分析に使用するため、よりXの因果効果に近い推定値を得られることが期待できる。
欠点:(観察可能な他の変数を統制してもなお)X = 1となるかどうかがランダムに生じていない場合には、Xの因果効果を推定することにはならない。サンプルサイズが小さくなる。
1時点前(3):1時点後にX = 1となっていないことが確認できる行についてのみ、1時点前ダミーの値を作成する。
この場合、1時点前ダミーの効果は、1行目、2行目、8行目、9行目を参照カテゴリとした場合の効果を意味する。
利点:サンプルサイズを確保しつつ、誤って1時点前でないと判断することを防いでいる。
欠点:解釈の難しさについては(1)とほぼ同じ。また、1時点前だけでなく、2時点、3時点前のダミーなどを作成する場合にはサンプルサイズは結局小さくなってしまう。
もちろん、独立変数のセンサリングの問題は、たとえ変化以前であることを考慮しないとしても同様に生じますが、考慮する場合にはさらにもう一つ考えることが増える、というイメージです。
また、個人内の偏差のみを分析に用いる固定効果モデルを用いる場合などだと、同一個人について比較をすることになるので、Xの変化以前の変数を投入したときの解釈の難しさについては多少緩和されると思います。
まとめ:XとYの関連に関する理論を立てる
以上のように、Yに対するXの効果が時間によって異なると想定することは、たんにXの値でYを比較するのとは異なるかたちでXとYの関連を考えることになります。こうすることによって、XとYの関連をより精緻に捉えることが可能になり得る一方で、たんにXの値でYを比較した場合のモデルよりも複雑さを持ち込むことになります。
基本的に、社会(科)学におけるモデルは、単純なほど望ましいでしょう。それでもなおより複雑なモデルを導入する際には、単にモデルの適合度が改善するというだけでなく、より良い理論的なインプリケーションが得られることを説得的に示すことが重要と考えます。Xの効果が時間によって変化するとは一体どのようなことを意味しているのか、XがどのようなメカニズムによってYを変化させるのか…に関する理論を考えることが重要と思います。